Pericyclic reaction

Example of a pericycle reaction: the norcaradiene–cyclohexatriene rearrangement

In organic chemistry, a pericyclic reaction is the type of organic reaction wherein the transition state of the molecule has a cyclic geometry, the reaction progresses in a concerted fashion, and the bond orbitals involved in the reaction overlap in a continuous cycle at the transition state. Pericyclic reactions stand in contrast to linear reactions, encompassing most organic transformations and proceeding through an acyclic transition state, on the one hand and coarctate reactions, which proceed through a doubly cyclic, concerted transition state on the other hand. Pericyclic reactions are usually rearrangement or addition reactions. The major classes of pericyclic reactions are given in the table below (the three most important classes are shown in bold). Ene reactions and cheletropic reactions are often classed as group transfer reactions and cycloadditions/cycloeliminations, respectively, while dyotropic reactions and group transfer reactions (if ene reactions are excluded) are rarely encountered.

Name	Bond changes
	Sigma	Pi
Electrocyclic reaction	+ 1	− 1
Cycloaddition (and cycloelimination)	+ 2	− 2
Sigmatropic reaction	0	0
Group transfer reaction	0	0
Ene reaction	+ 1	− 1
Cheletropic reaction	+ 2	− 1
Dyotropic reaction	0	0

In general, these are considered to be equilibrium processes, although it is possible to push the reaction in one direction by designing a reaction by which the product is at a significantly lower energy level; this is due to a unimolecular interpretation of Le Chatelier's principle. There is thus a set of "retro" pericyclic reactions.

Mechanism of pericyclic reaction

By definition, pericyclic reactions proceed through a concerted mechanism involving a single, cyclic transition state. Because of this, prior to a systematic understanding of pericyclic processes through the principle of orbital symmetry conservation, they were facetiously referred to as 'no-mechanism reactions'. However, reactions for which pericyclic mechanisms can be drawn often have related stepwise mechanisms proceeding through radical or dipolar intermediates that are also viable. Some classes of pericyclic reactions, such as the [2+2] ketene cycloaddition reactions, can be 'controversial' because their mechanism is sometimes not definitively known to be concerted (or may depend on the reactive system). Moreover, pericyclic reactions also often have metal-catalyzed analogs, although usually these are also not technically pericyclic, since they proceed via metal-stabilized intermediates, and therefore are not concerted.

Despite these caveats, the theoretical understanding of pericyclic reactions is probably among the most sophisticated and well-developed in all of organic chemistry. The understanding of how orbitals interact in the course of a pericyclic process has led to the Woodward–Hoffmann rules, a simple set of criteria to predict whether a pericyclic mechanism for a reaction is likely or favorable. For instance, these rules predict that the [4+2] cycloaddition of butadiene and ethylene under thermal conditions is likely a pericyclic process, while the [2+2] cycloaddition of two ethylene molecules is not. These are consistent with experimental data, supporting an ordered, concerted transition state for the former and a multistep radical process for the latter. Several equivalent approaches, outlined below, lead to the same predictions.

The aromatic transition state theory assumes that the minimum energy transition state for a pericyclic process is aromatic, with the choice of reaction topology determined by the number of electrons involved. For reactions involving (4n + 2)-electron systems (2, 6, 10, ... electrons; odd number of electron pairs), Hückel topology transition states are proposed, in which the reactive portion of the reacting molecule or molecules have orbitals interacting in a continuous cycle with an even number of nodes. In 4n-electron systems (4, 8, 12, ... electrons; even number of electron pairs) Möbius topology transition states are proposed, in which the reacting molecules have orbitals interacting in a twisted continuous cycle with an odd number of nodes. The corresponding (4n + 2)-electron Möbius and 4n-electron Hückel transition states are antiaromatic and are thus strongly disfavored. Aromatic transition state theory results in a particularly simply statement of the generalized Woodward–Hoffmann rules: A pericyclic reaction involving an odd number of electron pairs will proceed through a Hückel transition state (even number of antarafacial components in Woodward–Hoffmann terminology), while a pericyclic reaction involving an even number of electron pairs will proceed through a Möbius transition state (odd number of antarafacial components).

Equivalently, pericyclic reactions have been analyzed with correlation diagrams, which track the evolution of the molecular orbitals (known as 'correlating' the molecular orbitals) of the reacting molecules as they progress from reactants to products via a transition state, based on their symmetry properties. Reactions are favorable ('allowed') if the ground state of the reactants correlate with the ground state of the products, while they are unfavorable ('forbidden') if the ground state of the reactants correlate with an excited state of the products. This idea is known as the conservation of orbital symmetry. Consideration of the interactions of the highest occupied and lowest unoccupied molecular orbitals (frontier orbital analysis) is another approach to analyzing the transition state of a pericyclic reaction.

Arrow-pushing for pericyclic reactions

The arrow-pushing convention for pericyclic reactions has a somewhat different meaning compared to polar (and radical) reactions. For pericyclic reactions, there is often no obvious movement of electrons from an electron rich source to an electron poor sink. Rather, electrons are redistributed around a cyclic transition state. Thus, electrons can be pushed in either of two directions for a pericyclic reaction. For some pericyclic reactions, however, there is a definite polarization of charge at the transition state due to asynchronicity (bond formation and breaking do not occur to a uniform extent at the transition state). Thus, one direction may be preferred over another, although arguably, both depictions are still formally correct. In the case of the Diels-Alder reaction shown below, resonance arguments make clear the direction of polarization. In more complex situations, however, detailed computations may be needed to determine the direction and extent of polarization.

Pseudopericyclic processes

Closely related to pericyclic processes are reactions that are pseudopericyclic. Although a pseudopericyclic reaction proceeds through a cyclic transition state, two of the orbitals involved are constrained to be orthogonal and cannot interact. Perhaps the most famous example is the hydroboration of an olefin. Although this appears to be a 4-electron Hückel topology forbidden group transfer process, the empty p orbital and sp² hybridized B–H bond are orthogonal and do not interact. Hence, the Woodward-Hoffmann rules do not apply. (The fact that hydroboration is believed to proceed through initial π complexation may also be relevant.)

In biochemistry

Pericyclic reactions also occur in several biological processes:

• Claisen rearrangement of chorismate to prephenate in almost all prototrophic organisms
• [1,5]-sigmatropic shift in the transformation of precorrin-8x to hydrogenobyrinic acid
• non-enzymatic, photochemical electrocyclic ring opening and a (1,7) sigmatropic hydride shift in vitamin D synthesis
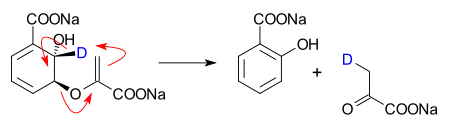
• Isochorismate pyruvate lyase catalyzed conversion of isochorismate into salicylate and pyruvate

See also

• Coarctate reaction
• Woodward–Hoffmann rules